OpenSCAD snippets
Table of Contents
For now, the snippets are self-contained.
That implies there may be duplicates of common functions between snippets.
Even worse, the functions with the same names may work differently in different snippets.
And there may be fewer comments than desired.
You’ve been warned ¯\_(ツ)_/¯
Wavy donut
Just why did I do this?
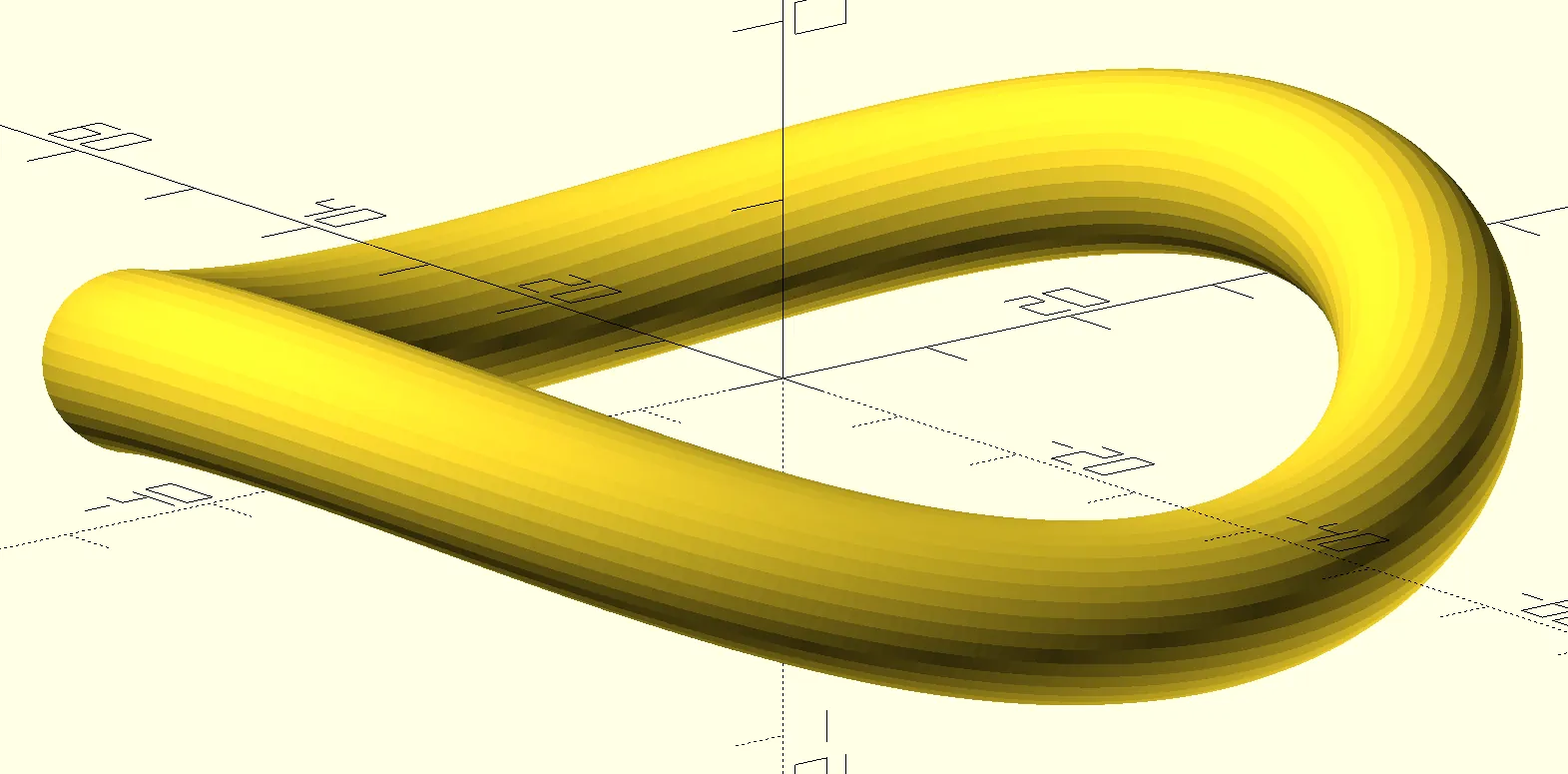
A render of the wavy donut with 2 waves
It is implemented using the polyhedron() OpenSCAD module.
I generate flat slices of the donut, rotate and position them in 3D using pts_rotate3 and pts_translate3, and then stitch them into a loop in the pts_extrude module.
There are alternative methods to get roughly similar results (e.g. intersecting cylinders or cones), but they are insufficient. Additionally, OpenSCAD’s boolean operations with polyhedra are not very fast. Smoothing the results with something like a Minkowski sum of the shape’s edge and a sphere would be painfully slow, and the result still won’t be as smooth as this.
What I really like about this one, is that it took me just a couple minutes to implement tilting of individual slices to make the waves actually «bend» rather than «bob». I used the fact that if \( f(\alpha) = cos(\alpha) \), and \( f(\alpha) \) is the slice «bobbing» function, then \( f'(\alpha) = -sin(\alpha) \) which provides the tilt. And then guesstimated some magic coefficients because I couldn’t be bothered.
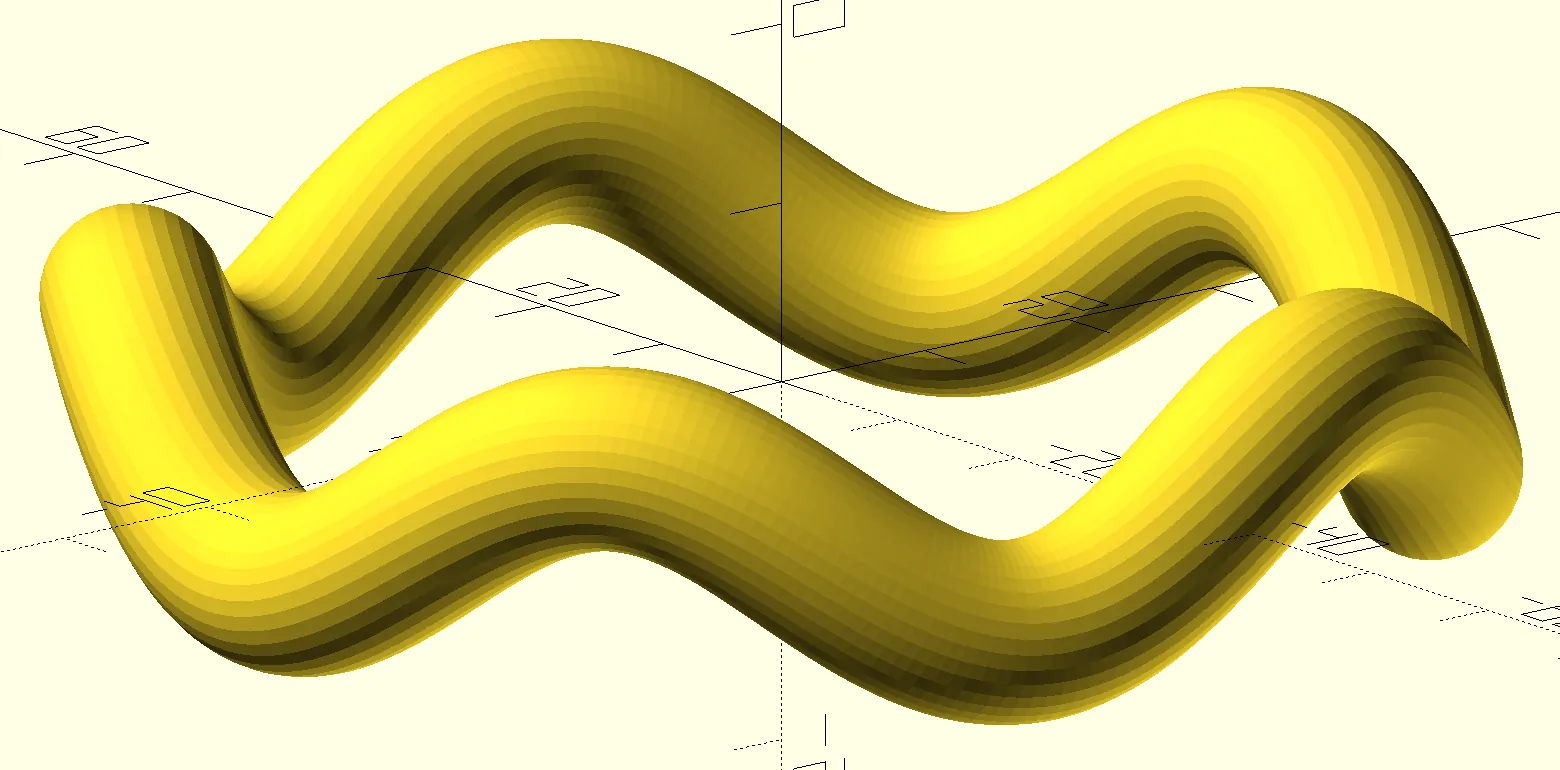
The same wavy donut, but with 5 waves
Source code of the wavy donut
function clamp(v_min, t, v_max) = max(v_min, min(t, v_max));
function pts_circle(radius, edges) =
assert(is_num(radius) && radius > 0, "'radius' is not a number larger than 0")
assert(is_undef(edges) || (is_num(edges) && edges > 2) , "'edges' is not a number larger than 2")
let(edges = is_num(edges) ? edges : clamp(12, radius, 360))
[ for (a = [0 : 360 / edges : 359.99999]) [cos(a) * radius, sin(a) * radius] ];
function _assert_vec2(vec) =
assert(is_list(vec) && len(vec) == 2, "a vec is not a list of 2 elements")
assert(is_num(vec.x) && is_num(vec.y), "a vec component is not a number")
true;
function _assert_vec3(vec) =
assert(is_list(vec) && len(vec) == 3, "a vec is not a list of 3 elements")
assert(is_num(vec.x) && is_num(vec.y) && is_num(vec.z), "a vec component is not a number")
true;
function _assert_flat(flat) =
assert(is_list(flat) && len(flat) > 2, "a flat is not a list of more than 2 points")
is_list([ for (point = flat)
assert(is_list(point) && len(point) == 2, "a point in a flat is not a list of 2 elements")
assert(is_num(point.x) && is_num(point.y), "a component of a point in a flat is not a number")
true
]);
function _assert_slice(slice) =
assert(is_list(slice) && len(slice) > 2, "a slice is not a list of more than 2 points")
is_list([ for (point = slice)
assert(is_list(point) && len(point) == 3, "a point in a slice is not a list of 3 elements")
assert(is_num(point.x) && is_num(point.y) && is_num(point.z), "a component of a point in a slice is not a number")
true
]);
function pts_translate2(flat, t) =
assert(_assert_flat(flat))
assert(_assert_vec2(t))
[ for (point = flat) point + t ];
function pts_translate3(slice, t) =
assert(_assert_slice(slice))
assert(_assert_vec3(t))
[ for (point = slice) point + t ];
function pts_inflate(flat) =
assert(_assert_flat(flat))
[ for (point = flat) [point.x, point.y, 0] ];
function pts_rotate3(s, r) =
assert(_assert_slice(s))
assert(_assert_vec3(r))
[ for (p0 = s)
let (
// 1. rotate around Z
p1 = [
p0.x * cos(r.z) - p0.y * sin(r.z),
p0.x * sin(r.z) + p0.y * cos(r.z),
p0.z,
],
// 2. rotate around Y
p2 = [
p1.x * cos(r.y) + p1.z * sin(r.y),
p1.y,
- p1.x * sin(r.y) + p1.z * cos(r.y),
],
// 3. rotate around X
p3 = [
p2.x,
p2.y * cos(r.x) - p2.z * sin(r.x),
p2.y * sin(r.x) + p2.z * cos(r.x),
]
) p3
];
module pts_extrude(slices) {
/* Validate the data */
// Check that 'slices' is a list of slices
assert(is_list(slices) && len(slices) > 2, "'slices' is not a list of more than 2 slices");
// Check that the first slice has enough points
assert(is_list(slices[0]) && len(slices[0]) > 2, "'slices[0]' is not a slice of more than 2 points");
_num_slices = len(slices);
_num_points = len(slices[0]);
// Check that all the slices have the same number of points
for (slice = slices) {
assert(is_list(slice) && len(slice) == _num_points, "a slice has a wrong number of points");
}
// Check that all slices contain points of right dimensionality
for (slice = slices) {
for (point = slice) {
assert(is_list(point) && len(point) == 3, "a point is not a list of 3 elements");
assert(is_num(point.x) && is_num(point.y) && is_num(point.z), "a point component is not a number");
}
}
/* Generate inputs */
// Collect all the points
points = [ for (slice = slices) each slice ];
// Define all the faces
faces = [ for (slice = [0 : _num_slices - 1]) each [
// For each slice, define rectangular faces that connect it to the next slice
for (i = [0 : _num_points - 1]) [
// Two points on the current slice
(slice * _num_points) + i,
(slice * _num_points) + (i + 1) % _num_points,
// Two points on the next slice (possibly zeroth)
((slice + 1) % _num_slices * _num_points) + (i + 1) % _num_points,
((slice + 1) % _num_slices * _num_points) + i,
]
] ];
/* Render */
polyhedron(points, faces);
}
module test() {
thickness = 10;
radius = 30;
delta_z = 10;
waves = 2;
fn1 = 36;
fn2 = 360;
function slice_tilt(t) = [- sin(waves * t * 360) * delta_z * waves * 2/3, 0, 0];
function slice_displacement(t) = [0, 0, cos(waves * t * 360) * delta_z / 2];
c_base = pts_translate3(
pts_rotate3(
pts_inflate(pts_circle(thickness / 2, fn1)),
[90, 0, 0]
),
[radius + thickness / 2, 0, 0]
);
cs = [ for (t = [1 / fn2 : 1 / fn2 : 1])
pts_translate3(
pts_rotate3(
pts_rotate3(
c_base,
slice_tilt(t)
),
[0, 0, t * 360]
),
slice_displacement(t)
)
];
pts_extrude(cs);
}
test();
Funky vase
A funky vase
I wanted to vary twist and scale while doing linear_extrude().
It’s possible to do that in something like ImplicitCAD.
In OpenSCAD, I had to assemble the end result from multiple slices, each of which had a fixed twist and scale value.
That also required correctly positioning and rotating the slices, so that they matched up with slices above and below.
Because of the boolean operations to merge the slices, this is one of the longest models to render in my collection, especially if you increase the resolution.
Source code of the funky vase
/**
Performs linear interpolation between values `v0` and `v1`.
Parameter `t` determines the weights of `v0` and `v1`.
Its valid values are in the interval [0, 1].
*/
function lerp(v0, v1, t) = assert(t >= 0 && t <= 1) (1 - t) * v0 + t * v1;
/**
Calculates a single point for a quadratic Bézier curve.
It has 3 control points.
Parameter `t` determines the extent from the start of the curve.
Its valid values are in the interval [0, 1].
*/
function _bezier2(pts, t) = lerp(lerp(pts[0], pts[1], t), lerp(pts[1], pts[2], t), t);
/**
Calculates a single point for a cubic Bézier curve.
It has 4 control points.
Parameter `t` determines the extent from the start of the curve.
Its valid values are in the interval [0, 1].
*/
function _bezier3(pts, t) = lerp(_bezier2([pts[0], pts[1], pts[2]], t), _bezier2([pts[1], pts[2], pts[3]], t), t);
// Height
h = 120;
// Sides of the base polygon
f = 6;
// Radius of the base polygon
r = 35;
// Slices
s = 36;
// Determines twist based on the slice
function t(sn) = _bezier3([0, 120, -180, 30], sn / (s - 1)) / s;
// Determines scale based on the slice
function e(sn) = _bezier3([1, 2, 0.5, 1.2], sn / s);
module __hidden__() {}
$fn = 12;
E = 0.01;
module rounden(r) {
offset(- r)
offset(r * 2)
offset(- r)
children();
}
module profile() {
circle(r, $fn = f);
module corners(r) {
for (a = [1 : f])
rotate(360 * a/f)
translate([r, 0]) {
circle(r / 3, $fn = f);
children();
}
}
corners(r)
corners(r / 3);
}
module vase() {
module slice(sn) {
twist = t(sn);
scale_start = e(sn);
scale_end = e(sn + 1) / scale_start;
scale([scale_start, scale_start, 1])
linear_extrude(h / s + E, slices = 4, twist = twist, scale = scale_end)
rounden(3)
profile();
rotate([0, 0, - twist])
translate([0, 0, h / s])
children();
}
module reslice(recur = 0) {
if (recur < s) {
slice(recur)
reslice(recur + 1)
children();
}
}
reslice();
}
vase();
Double helix loop with bridges
The thing
This builds up on the code written for the wavy donut. There are two strands, both of which are composed of slices that are transformed in various ways.
I also tried to implement slice tilt to make the cross-section round, like I kind of did for the wavy donut. However, I think I didn’t fully succeed, because I was struggling to find the right formulas (considering there is tilt on 2 axis & the phase shift between two strands). I don’t even know if it’s included in the following code (I think it is). But the shape still looks cool.
The bridges are, thankfully, just regular cylinders.
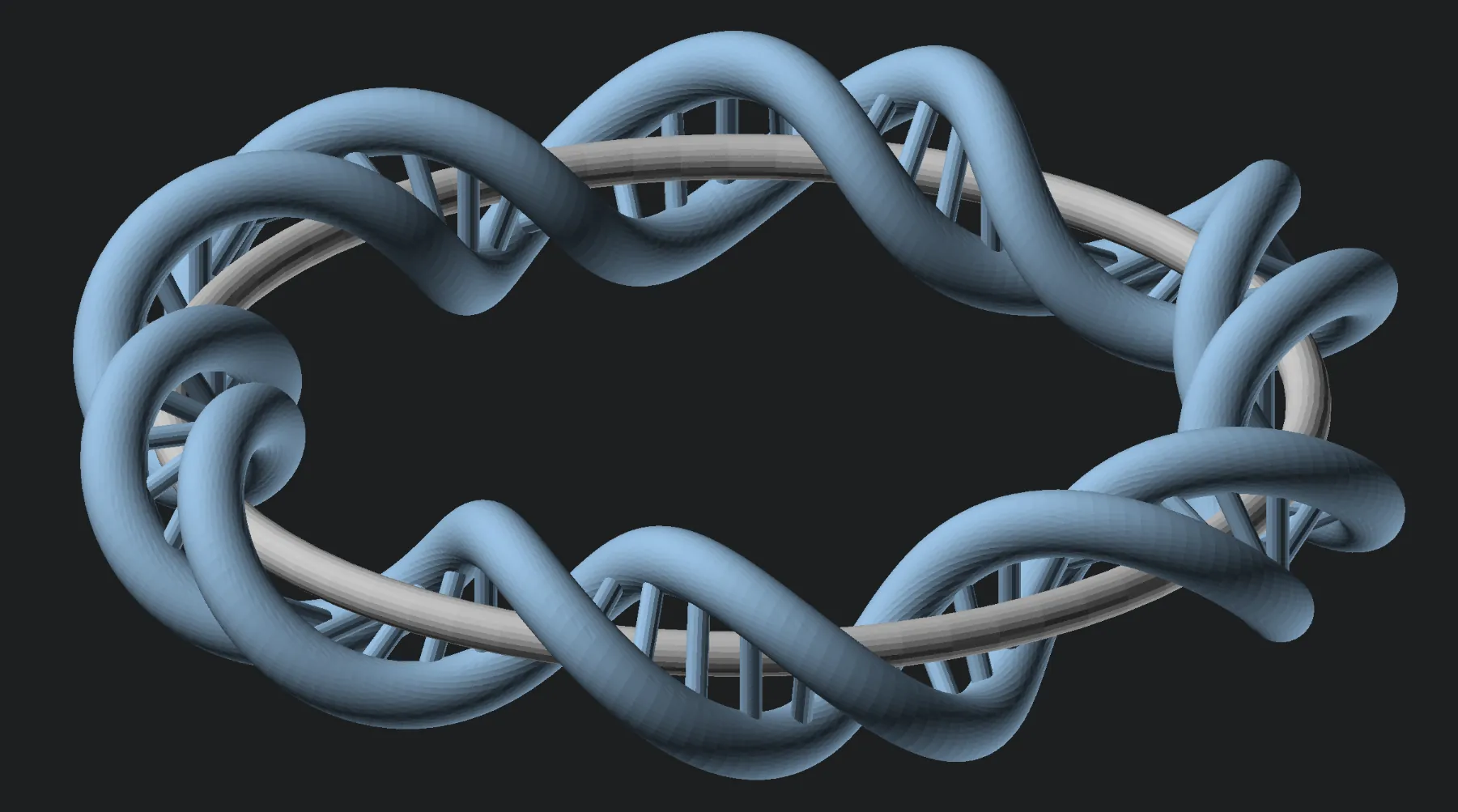
Here is what it looks like if I wrap it around a regular ring
Source code of the double helix loop with bridges
function _assert_vec3(vec) =
assert(is_list(vec) && len(vec) == 3, "a vec is not a list of 3 elements")
assert(is_num(vec.x) && is_num(vec.y) && is_num(vec.z), "a vec component is not a number")
true;
function _assert_flat(flat) =
assert(is_list(flat) && len(flat) > 2, "a flat is not a list of more than 2 points")
is_list([ for (point = flat)
assert(is_list(point) && len(point) == 2, "a point in a flat is not a list of 2 elements")
assert(is_num(point.x) && is_num(point.y), "a component of a point in a flat is not a number")
true
]);
function _assert_slice(slice) =
assert(is_list(slice) && len(slice) > 2, "a slice is not a list of more than 2 points")
is_list([ for (point = slice)
assert(is_list(point) && len(point) == 3, "a point in a slice is not a list of 3 elements")
assert(is_num(point.x) && is_num(point.y) && is_num(point.z), "a component of a point in a slice is not a number")
true
]);
function clamp(v_min, t, v_max) = max(v_min, min(t, v_max));
function pts_circle(radius, edges) =
assert(is_num(radius) && radius > 0, "'radius' is not a number larger than 0")
assert(is_undef(edges) || (is_num(edges) && edges > 2) , "'edges' is not a number larger than 2")
let(edges = is_num(edges) ? edges : clamp(12, radius, 360))
[ for (a = [0 : 360 / edges : 359.99999]) [cos(a) * radius, sin(a) * radius] ];
function pts_translate3(slice, t) =
assert(_assert_slice(slice))
assert(_assert_vec3(t))
[ for (point = slice) point + t ];
function pts_inflate(flat) =
assert(_assert_flat(flat))
[ for (point = flat) [point.x, point.y, 0] ];
function pts_rotate3(s, r) =
assert(_assert_slice(s))
assert(_assert_vec3(r))
[ for (p0 = s)
let (
// 1. rotate around Z
p1 = [
p0.x * cos(r.z) - p0.y * sin(r.z),
p0.x * sin(r.z) + p0.y * cos(r.z),
p0.z,
],
// 2. rotate around Y
p2 = [
p1.x * cos(r.y) + p1.z * sin(r.y),
p1.y,
- p1.x * sin(r.y) + p1.z * cos(r.y),
],
// 3. rotate around X
p3 = [
p2.x,
p2.y * cos(r.x) - p2.z * sin(r.x),
p2.y * sin(r.x) + p2.z * cos(r.x),
]
) p3
];
module pts_extrude(slices, loop = true, quads = true) {
/* Validate the data */
// Check that 'slices' is a list of slices
assert(is_list(slices) && len(slices) > 2, "'slices' is not a list of more than 2 slices");
// Check that the first slice has enough points
assert(is_list(slices[0]) && len(slices[0]) > 2, "'slices[0]' is not a slice of more than 2 points");
_num_slices = len(slices);
_num_points = len(slices[0]);
// Check that all the slices have the same number of points
for (slice = slices) {
assert(is_list(slice) && len(slice) == _num_points, "a slice has a wrong number of points");
}
// Check that all slices contain points of right dimensionality
for (slice = slices) {
for (point = slice) {
assert(is_list(point) && len(point) == 3, "a point is not a list of 3 elements");
assert(is_num(point.x) && is_num(point.y) && is_num(point.z), "a point component is not a number");
}
}
/* Generate inputs */
// Collect all the points
points = [ for (slice = slices) each slice ];
// If not loop, don't connect the last slice with the zeroth
_last_slice = loop ? _num_slices - 1 : _num_slices - 2;
// Define all the faces
faces = [ for (slice = [0 : _last_slice]) each [
// For each slice, define rectangular faces that connect it to the next slice
if (quads)
for (i = [0 : _num_points - 1])[
// Two points on the current slice
(slice * _num_points) + i,
(slice * _num_points) + (i + 1) % _num_points,
// Two points on the next slice (possibly zeroth)
((slice + 1) % _num_slices * _num_points) + (i + 1) % _num_points,
((slice + 1) % _num_slices * _num_points) + i,
]
else
for (i = [0 : _num_points - 1]) each [
[
// Two points on the current slice
(slice * _num_points) + i,
(slice * _num_points) + (i + 1) % _num_points,
// One point on the next slice (possibly zeroth)
((slice + 1) % _num_slices * _num_points) + (i + 1) % _num_points,
],
[
// One point on the current slice
(slice * _num_points) + i,
// Two points on the next slice (possibly zeroth)
((slice + 1) % _num_slices * _num_points) + (i + 1) % _num_points,
((slice + 1) % _num_slices * _num_points) + i,
]
]
]];
/* Render */
if (loop) {
polyhedron(points, faces, convexity = 10);
} else {
// Add closing faces
face_end_1 = [ for (i = [1 : _num_points]) _num_points - i ];
face_end_2 = [ for (i = [0 : _num_points - 1]) i + (_num_slices - 1) * _num_points];
faces = [ for (fs = [[face_end_1], faces, [face_end_2]]) each fs];
polyhedron(points, faces, convexity = 10);
}
}
module double_helix(
radius_ring,
radius_twist,
thickness,
gap,
twists,
fn_profile = 36,
fn_loop = 180,
) {
strand_base = pts_rotate3(
pts_inflate(pts_circle(thickness / 2, fn_profile)),
[90, 0, 0]
);
function trot(t) = twists * t * 360;
module strand(dx, dz) {
// The slice center will always be this far from the helix center
init_distance = sqrt(dx^2 + dz^2);
// Rotation of the init_distance to achieve dx and dz
init_angle = atan(dz / dx);
function slice_init(s, t) = pts_rotate3(
pts_translate3(
pts_rotate3(
s,
// Guesstimation to make the crossection more round
[- atan(1 / twists) * twists / 2, 0, 0]
),
[init_distance, 0, 0]
),
[0, init_angle, 0]
);
function slice_transform(s, t) = pts_translate3(
pts_rotate3(
slice_init(s, t),
[0, trot(t), 0]
),
[radius_ring, 0, 0]
);
strand_slices = [ for (t = [1 / fn_loop : 1 / fn_loop : 1])
pts_rotate3(
slice_transform(strand_base, t),
[0, 0, t * 360]
)
];
pts_extrude(strand_slices);
}
strand(radius_twist, (gap + thickness) / 2);
strand(radius_twist, - (gap + thickness) / 2);
}
module double_helix_bridges(
radius_ring,
radius_twist,
thickness,
gap,
twists,
steps
) {
$fn = 16;
module bridge() {
cylinder(gap, r = thickness / 2, center = true);
}
for (t = [1 / steps : 1 / steps : 1]) {
rotate([0, 0, t * 360])
translate([radius_ring, 0, 0])
rotate([0, twists * t * 360])
translate([radius_twist, 0, 0])
bridge();
}
}
/* Parameters */
radius_ring = 25;
radius_twist = 2;
gap = 4;
twists = 6;
bridges = 72;
thickness_helix = 3;
thickness_bridge = 1;
/* Render */
double_helix(
radius_ring = radius_ring,
radius_twist = radius_twist,
thickness = thickness_helix,
gap = gap,
twists = twists,
fn_loop = 360
);
double_helix_bridges(
radius_ring = radius_ring,
radius_twist = radius_twist,
thickness = thickness_bridge,
gap = gap + thickness_helix / 2,
twists = twists,
steps = bridges
);